Gitterschalen
Tragverhalten und Verformung, Ausbildung und gebaute Beispiele
Schalen sind gekrümmte Flächentragwerke, die im Gegensatz zur Seillinienbelastung oder Stützlinienbelastung beliebige stetig verteilte Lasten über Membrankräfte tragen können. Sie haben „aufgrund ihrer Form ein besonders günstiges, ja geradezu ideales Trageverhalten, das sich in einem geringen Materialverbrauch ausdrückt.“ Sie sind in den meisten Fällen „schön als Folge der natürlichen Eleganz von Tragwerken, deren Form sich logisch aus dem Kraftfluss entwickelt. Ihr Tragwerk ist identisch mit dem Bauwerk und deshalb entsteht ihre Form aus ihrer Funktion“. [1]
Gallerie
Der momentenfreie Beanspruchungszustand einer Schale wird als Membranspannungszustand bezeichnet, die Lastabtragung erfolgt durch Normal- und Schubkräfte. Diese Effektivität ermöglicht dünne Schalen, die aufgrund geringer Biegesteifigkeit jedoch zur Aufnahme von Biegebeanspruchungen kaum geeignet sind. Hohe Biegebeanspruchungen führen zum Versagen von Schalentragwerken. Beim Entwerfen von Schalen muss daher zur Vermeidung von Biegebeanspruchungen eine konstruktive Disziplin in Bezug auf Geometrie, Belastung und Randbedingungen eingehalten werden.
Geringe Schalenverformung ist anzustreben
Das Grundprinzip lautet: Da Normal- und Schubkraftverformungen im Vergleich zu Biegeverformung minimal sind, müssen Gleichgewichts- und Verträglichkeitsbedingungen für die Gültigkeit des Membranzustandes von Schalen so beachtet werden, dass geringe Schalenverformungen entstehen. Das Gleichgewicht wird gewährleistet durch die Stetigkeit in Verlauf, Steigung und Krümmung der Schalenmittelfläche und die Stetigkeit der Verteilung der Flächenlast sowie die unverschiebliche und tangentiale Auflagerung am Schalenrand. Die Verträglichkeit wird gewährleistet durch die Vermeidung einer sprunghaften Veränderung der Schalendicke, durch die geringe Welligkeit der Geometrie und der Belastung und durch die Vermeidung von Verformungsbehinderungen der Schalenränder. Dünne Schalen liegen dann vor, wenn in Abhängigkeit von der Schalendicke (h) und der Mindestradien (r) gilt: 1/1000 < h/r > 1/20 [2]. Werden Gleichgewicht und Verträglichkeit verletzt, müssen im Bereich dieser Verletzungen Biegetragstrukturen mit den entsprechend notwendigen Biegesteifigkeiten ausgebildet werden.
Schalen neigen zum Beulen, einem globalen Stabilitätsversagen der Gesamtschale. Dadurch unterscheiden sie sich von druckbeanspruchten, knickgefährdeten Stäben. Der perfekte, elastische Stab (ε = 0) verzweigt indifferent unter der Knicklast PK0 (Theorie II. Ordnung). Das Last-Verformungs-Diagramm des imperfekten, elastischen Stabes (e¹ 0) nähert sich asymptotisch an das Last-Verformungs-Diagramm des perfekten, elastischen Stabes an. Das maximale Lastniveau ist dabei immer durch die Knicklast PK0 definiert. Letztlich versagt der Knickstab durch Materialversagen infolge der Überschreitung der zulässigen Biegespannung. Demgegenüber verzweigt der perfekte, elastische Zylinder (e = 0) vom primären Ast (Vorbeulbereich; klassische, lineare Stabilitätstheorie; Linie 1) im Verzweigungspunkt PK0 in einen sekundären Ast (Nachbeulbereich) mit gleichzeitigem Abfall der aufnehmbaren Last F (bösartiges Nachbeulverhalten). Für ein beliebiges Lastniveau existieren dadurch mehrere Gleichgewichtslagen – im perfekten und im gebeulten imperfekten Zustand.
Beulen und Imperfektionsempfindlichkeiten
Eine perfekte, druckbeanspruchte Halbkugel beispielsweise beginnt auf dem Lastniveau der Verzweigungslast zu beulen und beult im Extremfall so lange, bis ein um den unverschieblichen Auflagerring nach unten gespiegeltes, zugbeanspruchtes „Tuch” das Lastniveau, weil es nicht mehr beult, wieder aufnehmen kann. Wird eine Imperfektion der Schale vorausgesetzt und auch notwendigerweise angesetzt, entsteht ein Durchschlagproblem und kein Verzweigungsproblem mehr. Die Durchschlaglasten (PK1 bzw. PK2) der imperfekten, elastischen Zylinderschale (e ¹ 0) betragen nur einen Bruchteil der Verzweigungslast PK0. Die Art und Größe der Imperfektion hat unmittelbaren Einfluss auf die Höhe der Durchschlaglast PK1 bzw. PK2. Größere Imperfektionen (e2> e1) ergeben niedrigere aufnehmbare Lasten PKn. Schalen sind also imperfektionsempfindlich.
Grundsätzlich lässt sich feststellen, dass hohe Beulsteifigkeiten geometrisch perfekter Schalen, d.h. hohe Verzweigungslasten PK0, große Imperfektionsempfindlichkeiten zur Folge haben. Weil die Form des hyperbolischen Paraboloids immer zug- und druckbeansprucht wird und sich durch die Zugbeanspruchung selbst stabilisiert, weist sie die geringsten Imperfektionsempfindlichkeiten auf. Die Kugel dagegen weist eine vielfache Beulsteifigkeit der perfekten Schale auf, ist aber am imperfektionsempfindlichsten.
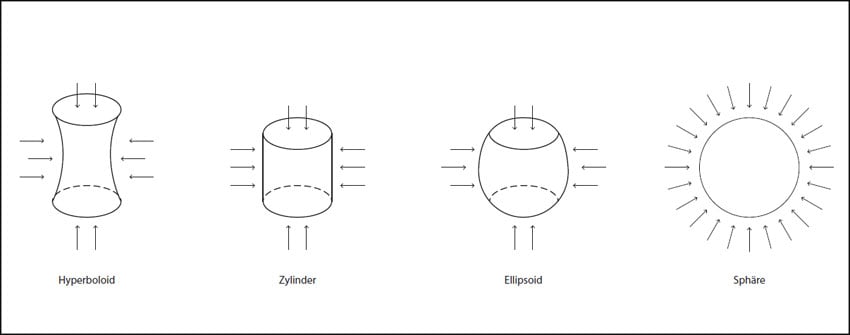
Imperfektionsempfindlichkeit von unter konstantem Außendruck
belasteten Schalenformen; Abb.: Baunetz (si), Berlin
Die eigentliche Aufgabe der Stabilitätsuntersuchung liegt daher im
Auffinden der kritischen Last PKn und damit im Auffinden
der maßgebenden Imperfektionsfigur. Eine Möglichkeit zur Auffindung
der maßgebenden Imperfektionsfigur wird in [3] (s.u.
Quellenangaben) aufgezeigt.
Herstellung und Ausbildung von Gitterschalen
Im Holzbau werden Schalen üblicherweise aus stabförmigen Bauteilen als Gitterschalen erstellt. Digitale Konstruktionswerkzeuge und automatisierte Vorfertigungstechnologien erlauben in jüngerer Zeit auch flächig doppeltgekrümmte oder polygonal gekrümmte Konstruktionen aus Brettsperrholz. Stäbe von doppeltgekrümmten Gitterschalen sind verdreht und einfach oder doppelt gekrümmt. Die Herstellung solcher Schalen ist entsprechend aufwändig.
Grundprinzip von Gitterstrukturen zur Erlangung des Schalentragverhaltens ist die Ausbildung von „Dreiecksmaschen”. Dadurch können die bei gekrümmten Flächentragwerken entstehenden Membrankräfte, Normalkräfte und Schubkräfte auch in aufgelösten Gitterstrukturen aufgenommen werden. Das heißt, Stabscharen sind in drei verschiedene Schalenrichtungen auszubilden, wie z.B. in Europas größter Holzkuppel des Salzlagers in Pratteln mit 120 Metern Durchmesser (Schweiz, 2012). Alternativ ist es auch möglich, zwei Stabscharen und eine flächige Dachschalung, die dann als dritte Stabschar wirkt, auszubilden – siehe z.B. die in Ringrichtung verlaufende Dachschalung der Lamellenkuppel der Neue Messe Rimini.
Die Grundstrukturen von Schalentragwerken sind Tonnenschalen, Kuppeln, Hyparschalen und Freiformflächen. Tonnenförmige Gitterschalen aus Holz werden üblicherweise mit in Schraubenlinien schräg über die Tonne verlaufenden Lamellen erstellt. Zwei gegenläufige Lamellenscharen bilden rautenförmige Maschen aus. Je schräger die Lamellen, desto verwundener ihre Stabachse. Diese nach Friedrich Zollinger benannte Zollbauweise wurde ab den 1920er-Jahren gebaut. Entlang der Schraubenlinie sind Krümmung und Verwindung konstant, daher können durch die Wahl gleicher Stablängen alle Stäbe einer Drehrichtung identisch ausgebildet werden. Zollinger stößt immer zwei Lamellenenden auf eine durchgehende Lamelle. Der Anschluss der Lamellenenden erfolgte ursprünglich mit einem, später mit zwei Schraubenbolzen, die die Schmiegen an den durchgehenden Stab anpressen. Um diese einfache Verbindung realisieren zu können, sind bei der Zollbauweise die gestoßenen Stäbe im Knoten versetzt zueinander angeordnet. Die kontinuierliche Verwindung des Stabes ist nur in den Schmiegeschnitten der Lamellen berücksichtigt worden, entlang der Lamelle wurde oberseitig die Krümmung eingestellt. Die Aussteifung der rautenförmigen Maschen erfolgte mit einer außenliegenden Holzverschalung, aussteifende Binder wurden lediglich an den Giebelseiten angebracht. Der Holzverbrauch sowie der Montageaufwand waren im Vergleich zu anderen Dachkonstruktionen deutlich geringer.
Das konstruktive Problem der Zollbauweise lag in den versetzten Anschlüssen der druckbeanspruchten Stäbe, die im durchgehenden Stab Querbiegebeanspruchungen erzeugten. Dies führte zusätzlich zu auftretenden Schwindverkürzungen zum Biegekriechen des durchgehenden Stabes und damit im Laufe der Zeit zu großen Verformungen der Tonnenschalen.
Biegebeanspruchung von Tonnenschalen
An den Traufkanten kontinuierlich gelagerte Tonnenschalen verformen sich unter halbseitigen Lasten ähnlich wie Bogentragwerke, da sie in die Ebene abwickelbare Flächen sind. Das heißt dann auch, dass bei nicht stützlinienaffinen Lasten Biegebeanspruchungen in der Tonnenschale entstehen. Bei der Zollbauweise konnten diese Biegebeanspruchungen bei einer Verschraubung im Knoten gar nicht und bei zwei Schrauben je Knoten nur in geringem Maße aufgenommen werden. Dadurch musste jeweils der im Knoten durchgehende Stab, da er schräg zur Momentenbeanspruchung steht, Biegung und Torsion aufnehmen. Torsionsbeanspruchungen sind beim Werkstoff Holz jedoch zu vermeiden, weil ein Holzstab sich unter Torsion durch Kriechverformungen verwindet und sich damit der Beanspruchung entzieht (Abb. 3).
Sollen die Biegeverformungen aus halbseitiger Last und damit auch die Biegebeanspruchungen stark eingeschränkt werden, sind Queraussteifungen der Tonnenschalen in regelmäßigen Abständen erforderlich. Solche Queraussteifungen können neben biegesteifen Bögen mit Zugbändern z.B. die in der Abbildung unten dargestellten Seilverspannungen sein, die allesamt auf dem Prinzip von Šuchov aufbauen. Der russische Ingenieur Vladimir Šuchov entwarf 1896 für die 15 Meter weit spannende, tonnenförmige Überdachung des Einkaufszentrums GUM in Moskau ein seilverspanntes stählernes Bogentragwerk. Die Grundidee war, die Verformung des Bogens unter nicht stützlinienaffinen Lasten durch Seile zu verhindern, die jeweils von den unverschieblichen Auflagern zur gegenüberliegenden Bogenhälfte spannen. Letzten Endes mussten auch die heute unter Denkmalschutz stehenden Zollingerdächer durch Verstärkungen in Querrichtung saniert werden.
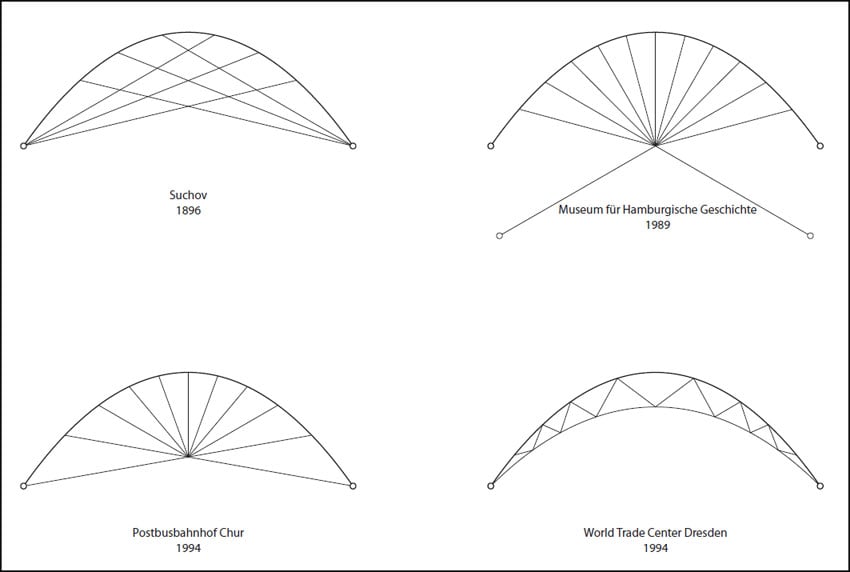
Mögliche Queraussteifungen von Tonnenschalen; Abb:
Baunetz (si), Berlin
Ein Beispiel der nach der Zollbauweise entworfenen rautenförmigen
Tonnenschale ist die 60 Meter weit spannende Holzkonstruktion der
Neue Messe Rimini. Jeweils vier Holzstäbe treffen sich
werkstoffgerecht zentral in einem Knoten, um die negativen
Wirkungen exzentrischer Anschlüsse im Holzbau zu vermeiden. Die
Queraussteifung für nicht stützlinienaffine Lasten erfolgt über
sichelförmige, fachwerkartige Unterspannungen.
Schwedlerkuppel und geodätische Kuppel
Zu den synklastisch gekrümmten Kuppeln gehören die Lamellenschalen und die Schwedlerkuppel, die nach J. W. Schwedler benannt ist, sowie die geodätische Kuppel. 1863 vollzog Schwedler bei der Überdachung von zylindrischen Gasbehältern den Schritt zum echten Schalentragwerk. Bei der Schwedlerkuppel steifen Diagonalstäbe die in Meridian- und Ringrichtung verlaufenden Stabscharen aus. Meridian- und Ringstäbe bilden dabei viereckige Maschen. Zum Schalentragwerk wird diese Kuppel durch die Schar an Diagonalstangen, die die Vierecksmaschen in steife Dreiecksmaschen umwandeln. Da diese Stangen nur Zug übertragen können, müssen in jeder Vierecksmasche Diagonalauskreuzungen eingebaut werden.
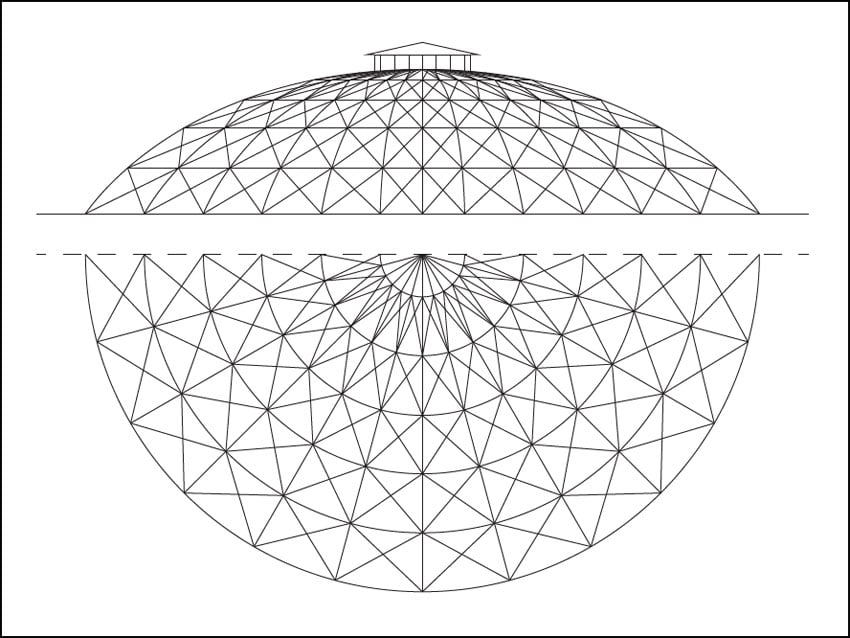
Systemskizze einer Schwedlerkuppel; Abb: Baunetz (si),
Berlin
Die geodätische Kuppel wurde von Walther Bauersfeld bei der
Bewehrungsführung von kugelförmigen Betonschalen erfunden und
zusammen mit Franz Dischinger bei der Versuchskuppel auf dem
Firmengelände der Firma Zeiss in Jena 1922 umgesetzt. Die
Stabeinteilung der Bewehrung entspricht einer vom Ikosaeder
abgeleiteten Netzschalenstruktur. Der Ikosaeder ist ein aus 20
gleichseitigen Dreiecken bestehender platonischer Körper. Werden
die Dreiecksflächen von innen auf die umschriebene Kugelform
projiziert, erhält man 20 sphärisch gleichseitige Großdreiecke.
Diese Großdreiecke werden wiederum in dreieckige Stabnetze
eingeteilt, wobei sich immer sechs Stäbe in einem Knoten treffen.
Die Treffpunkte der Großdreiecke führen immer zu fünf Stäben je
Knoten. Charakteristisch sind die geschwungenen Ränder in der
Kuppelansicht. Die Versuchskuppel auf dem Firmengelände der Firma
Zeiss in Jena entspricht einer Halbkugel mit 16 Metern Durchmesser
und einer nur sechs Zentimeter starken Betonschale.
Bei der kurz nach der Versuchskuppel 1924 von Bauersfeld und Dischinger gebauten 40 Meter weit spannenden Schale über dem Firmengelände der Firma Schott wurde auch nur eine Schalendicke von sechs Zentimetern ausgeführt. Die Tragfähigkeits- und Ressourceneffizienz der Schalentragwerke wird im Dicken (h)/Spannweiten (L)-Verhältnis deutlich. Für die Schale der Firma Schott beträgt das h/L-Verhältnis: h/L = 6/4000 = 1/667. Das ist im Vergleich zu den Biegeträgern und auch den Fachwerkträgern mit h/L = 1/12 – 1/15 eine Erhöhung der Schlankheit um ca. den Faktor 50.
Hyparschalen: Tragverhalten und Besonderheiten
Hyperbolische Paraboloidschalen, auch Hyparschalen genannt, sind antiklastisch gekrümmte Flächentragwerke, die in den parabelförmigen Haupttragrichtungen zug- und druckbeansprucht sind. Hängende Parabeln nehmen Zug auf, stehende Parabeln Druck. Die Hyparschale ist für beliebige, stetig verteilte Lasten frei von Biegebeanspruchungen und unterscheidet sich damit grundlegend vom Tragverhalten eines Bogens bzw. eines Zugbands. Beim Membrantragverhalten werden Biegebeanspruchungen dadurch vermieden, dass die nicht stützlinien- bzw. seillinienaffinen Lasten der Haupttragrichtungen zusätzlich über Schubkräfte in der Schalenfläche abgetragen werden. Als Gitterschale ausgebildet, bedeutet dies die Ausbildung räumlicher Stabdreiecke, wobei die Stäbe dann rein zug- oder druckbeansprucht sind. Alternativ kann die zur Schalentragwirkung notwendige dritte Stabschar auch aus einer Dachschalung oder aus gekreuzten Seildiagonalen bestehen.
Eine weitere geometrische Besonderheit von Hyparschalen ist die Tatsache, dass über gerade Erzeugende die antiklastische Fläche gebildet werden kann. Die Herstellung wird durch die Verwendung von geraden Brettern, die entlang der Erzeugenden verwunden werden müssen, auf einfache Art möglich.
Die Ränder der Hyparschale „sammeln” die Dachlasten aus den Zug- und Druckkräften der Gitterstäbe entlang der Randträger auf und leiten diese von den Hochpunkten zu den Auflagerpunkten ab. Daher können Hyparschalen mit geraden Rändern, wenn das Kippen um die Tiefpunkte der Auflager ausgeschlossen ist, an nur zwei Punkten der Schalenkonstruktion auflagern. Wesentliche Vertreter dieser Schalenbauweise waren Félix Candela und Ulrich Müther. Da die Ränder die Gesamtlasten der Gitterschale abzuführen haben, sind sie im Vergleich zur Schalenfläche hoch beansprucht. Sie wirken im Tragverhalten wie gerade oder gebogene Stäbe mit Längsbeanspruchung. Als Stabtragwerke sind sie durch ihr Eigengewicht und durch Umlenkkräfte zusätzlich zur Normalkraftbeanspruchung auch biege- und querkraftbeansprucht. Der Querschnitt der Schalenränder muss für eine ausreichende Tragfähigkeit entsprechend hoch im Vergleich zum Schalenquerschnitt ausfallen.
Experimentelle Formfindung
Freiformflächen sind, wie der Name schon sagt, frei geformte Flächen. Dies bedeutet aber nicht, dass damit automatisch ein Schalentragverhalten ableitbar ist. Vielmehr müssen auch Freiformflächen für die Gültigkeit des Membranspannungszustandes die oben genannten Gleichgewichts- und Verträglichkeitsbedingungen von Schalen einhalten. Bei Freiformflächen, die beispielsweise durch architektonische Formsetzungen gefunden wurden, wäre ein Membranspannungszustand reiner Zufall. Vielmehr sind bei solchen Schalenformen Biegebeanspruchungen vorhanden, die durch biegesteife Gitterstäbe aufzunehmen sind. Filigrane Gitterschalen als Freiformflächen entstehen nur durch experimentelle oder mathematisch-numerische Formfindungsmethoden – wie Werner Sobek definiert, „Formentwicklungsmethoden” [4] – die lediglich normalkraft- und schubkraftbeanspruchte Bauteile hervorbringen.
Berühmte Betonschalen, deren Formen experimentell durch Hängemodelle gefunden wurden, sind vom Schweizer Ingenieur Heinz Isler ab der Mitte des 20. Jahrhunderts gebaut worden. Für den Holzbau prägend war die 1975 fertiggestellte Multihalle in Mannheim von Frei Otto und Carl Friedrich Mutschler (Abb. 1,2), eine ebenfalls im Hängemodell gefundene Freiformfläche. Durch Spiegelung an einer Horizontalebene wird das rein zugbeanspruchte Seilnetz zum rein druckbeanspruchten Gitternetz.
Die Holzgitterschale der Multihalle Mannheim besteht aus zwei Scharen dünner Latten. Da das Seilnetz als Hängemodell für lediglich einen Lastzustand die Gleichgewichtsform darstellt, sind für veränderliche Lasten zusätzlich zum Gitternetz Diagonalen, d.h. Dreiecksmaschen auszubilden. Da dies bei der Multihalle nicht für jede Netzmasche gewollt war, wurden zur Aufrechterhaltung des Schalentragverhaltens neben großräumigen Diagonalauskreuzungen in den Kreuzungspunkten der Maschen außerdem biegesteife Knoten über Reibungsdruck von Federscheiben, die auf die Knoten drücken, ausgebildet. Die Gitterstäbe wurden dadurch zusätzlich zur Druckkraftbeanspruchung in der Schalenfläche biegebeansprucht. Da Holz unter konstanten Querdruckbeanspruchungen kriecht (Abb. 3), sind über die Jahrzehnte die Wirkungen der Biegesteifigkeiten kaum mehr vorhanden. Dies hatte zur Folge, dass inzwischen große Verformungen der Gitterschale eintraten. Um einen Einsturz zu vermeiden, wird das baukulturelle Denkmal ab voraussichtlich 2020 saniert.
Quellenangaben: [1] Schlaich, J., 1982: Haben Betonschalen eine Zukunft? Sonderdruck aus „beton“ 32, Heft 9, Düsseldorf : Beton-Verlag, S. 327 – 332). [2] Ramm, E. ; Müller, J., 2001: Schalen. Vorlesungsmanuskript, Stuttgart, Universität, Institut für Baustatik. [3] Graf, J., 2002: Entwurf und Konstruktion von Translationsnetzschalen. Dissertation. Stuttgart, Universität, Institut für Konstruktion und Entwurf II. Verlag Grauer, Beuren. [4] Sobek, W., 2007. Entwerfen im Leichtbau. In: Leichtbau – Themenheft Forschung No 3. Universität Stuttgart. Alpha Informationsgesellschaft mbH, Seite 70 ff.
Fachwissen zum Thema
Baunetz Wissen Holz sponsored by:
Informationsdienst Holz | getragen durch den Informationsverein Holz, Düsseldorf
Kontakt: +49 (0) 211 9665580 | info@informationsvereinholz.de
und Holzbau Deutschland Institut e.V., Berlin
Kontakt: +49 (30) 20314533 | kontakt@institut-holzbau.de
und Studiengemeinschaft Holzleimbau e.V., Wuppertal
Kontakt: +49 (0) 20276972732 | info@studiengemeinschaft-holzleimbau.de









































