_Mauerwerk
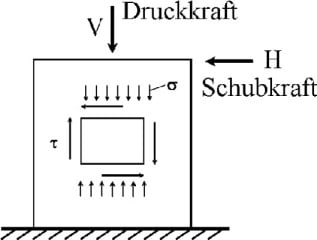
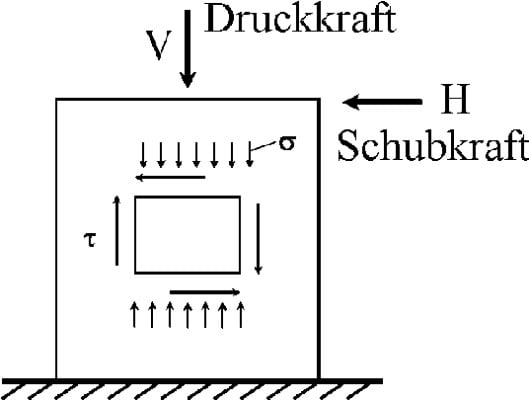
Belastung durch Schubkräfte
Die Beschreibung des Schubtragverhaltens von unbewehrtem
Mauerwerk erfolgt allgemein nach dem Modell von Mann/Müller.
(Grundlage der von Mann/Müller entwickelten Schubbruchtheorie
für Mauerwerkswände ist die Belastung einer Wandscheibe durch
Normal- und Querkräfte). Hierbei werden insgesamt vier
Bruchbedingungen formuliert, die auch Basis der Schubbemessung der
aktuellen deutschen Mauerwerksnorm DIN 1053-1 sind. Die Theorie
wurde durch Vergleiche mehrerer Autoren mit Versuchsergebnissen
überprüft und es ergab sich im Allgemeinen eine gute bis sehr gute
Übereinstimmung.
Folgende Materialparameter gehen in die Beschreibung des
Schubtragverhaltens ein:
- Mauerwerksdruckfestigkeit (senkrecht zu den Lagerfugen)
βmw
- Steinzugfestigkeit βz,st
- Haftscherfestigkeit des Mörtels k
(Kohäsion)
- Reibungsbeiwert der Lagerfuge μ
- Verhältnis von Steinhöhe zu Steinlänge Δx/Δy
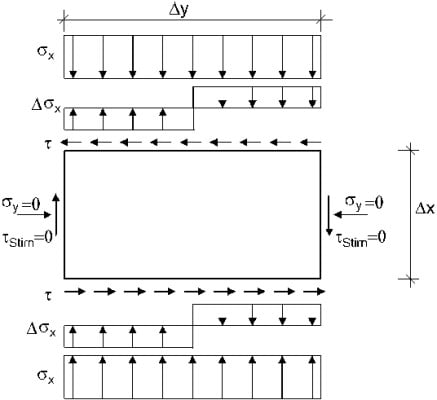
Für die Untersuchung der Spannungsverteilung an einem Einzelstein wird ein Element der Wandscheibe herausgeschnitten und die angreifenden Spannungen angetragen. Die vom Betrag her relativ kleinen Druck- und Zugspannungen in Richtung der Lagerfugen werden in diesem Modell vernachlässigt.
Da in den Stoßfugen keinerlei Spannungen übertragen werden können, muss das Moment infolge angreifender Schubspannungen durch eine blockförmige Verteilung der Normalspannungen in der Lagerfuge ausgeglichen werden.
Zusammen mit den mittleren Normalspannungen senkrecht zu den Lagerfugen σx infolge der vorhandenen Vertikalauflast ergeben sich mit den blockförmig verteilten Normalspannungen σ1,2= σx+(-)τ*2*Δx/Δy folgende vier Versagenskriterien:
- Für das Reibungsversagen in der Lagerfuge wird die Steinhälfte mit der geringeren Normalspannung σ2=σx–τ*2*Δx/Δy maßgebend. Es ergibt sich eine maximale aufnehmbare Schubspannung τ=k+μ*σ2
- Infolge der angreifenden Schub- und Normalspannungen 2τ und
σx ergeben sich in Steinmitte schiefe
Hauptzugspannungen, die beim Überschreiten der Steinzugfestigkeit
zum Steinversagen führen.
Als maximale Schubspannung ergibt sich: τ=βz,st/2,3*(1+σx/βz,st)1/2 - In der Steinhälfte mit der höheren Normalspannung σ1
kommt bei Überschreitung der Mauerwerksdruckfestigkeit
βmw zum Druckversagen.
Zurückgerechnet auf die Schubspannung ergibt sich τ=(βmw-σx)*Δy/(2*Δx) - Bei geringen Normalspannungen kann die Spannung σ2
die Haftzugfestigkeit überschreiten. Es kommt zum Klaffen in der
Lagerfuge. Für die übliche Bemessung ist dieser Fall durch den
Ansatz der Kohäsion abgedeckt.
Fachwissen zum Thema
Kontakt Redaktion Baunetz Wissen: wissen@baunetz.de
Baunetz Wissen Mauerwerk sponsored by:
KS-ORIGINAL GmbH
Entenfangweg 15
30419 Hannover
www.ks-original.de
KS-ORIGINAL GmbH
Entenfangweg 15
30419 Hannover
www.ks-original.de
